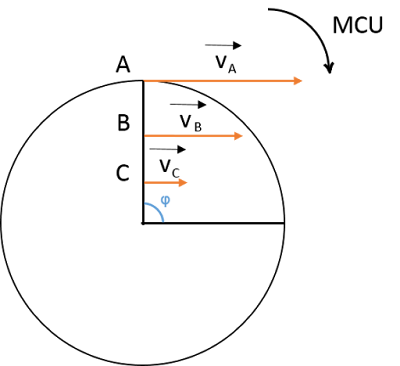Movimiento Circular Uniforme (MCU)

Física ⇒ Cinemática ⇒ Movimiento Circular Uniforme (MCU)
Ecuación

φ = φ0 + ω · t
  • ω = velocidad angular
  • φ = ángulo final
  • φ0 = ángulo inicial
Los ángulos girados son proporcionales al tiempo transcurrido. Es análoga a la ecuación s = v · t del MRU, si sustituímos el espacio s por el ángulo φ y la velocidad de traslación v, o velocidad lineal, por la velocidad angular ω.

Características del MCU
Decimos que una partícula material se desplaza con movimiento circular uniforme cuando:
  • describe una trayectoria circular
  • y su velocidad v→ es constante en módulo, pero no en dirección.

movimiento circular uniforme


En una partícula que gira con MCU, el vector v→ mantiene constante el módulo pero no la dirección ya que, al ser ésta tangente a la circunferencia, debe cambiar constantemente. Por tanto:
  • como no cambia el módulo de v→, no hay aceleración tangencial, at→
  • por cambiar la dirección de v→, hay aceleración normal, an→


Aceleración Normal
Llamamos aceleración normal a la aceleración debida al cambio que experimenta la dirección del vector velocidad.
La aceleración normal an→ es un vector perpendicular al vector velocidad v→ y dirigido hacia el centro de la circunferencia, por lo que también se llama aceleración centrípeta, y su módulo vale:

an =
v2 / r
  • an: aceleración normal o centrípeta
  • r = radio de giro de la partícula
La ecuación de dimensiones de la aceleración normal es :
  • [an] =
    [v]2 / [r]
    =
    (L · T-1)2 / L
    = L · T-2


Velocidad Angular

velocidad angular


Está claro que en cierto intervalo de tiempo, los puntos A, B y C han realizado unos desplazamientos distintos, por lo que las velocidades de las partículas A, B y C también serán distintas. Concretamente A gira a mayor velocidad que B y éste a más velocidad que C.
Así pues, como los puntos de un mismo radio se mueven cada uno a una velocidad distinta de la de los demás, resulta que no podemos expresar la velocidad del conjunto usando la velocidad de traslación ya que ésta varía de un punto a otro. Para ello usamos un nuevo concepto:
La velocidad angular de un sólido en rotación es la razón entre el ángulo descrito por un radio perpendicular al eje de giro y el tiempo empleado en describir dicho ángulo.
  • ω =
    φ / t
Esta magnitud permite describir al mismo tiempo y mediante un valor único, tanto el movimiento de rotación del sólido como el de cada una de las partículas que lo forman, ya que ω es común para todas ellas.
Un sólido en rotación gira con movimiento circular uniforme cuando su velocidad angular es constante.


Relación entre las velocidades lineal y angular
La velocidad lineal de una partícula es igual al producto de su velocidad angular por el radio de giro.

  • v = ω · r

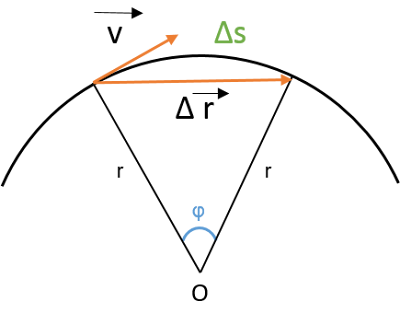
Para deducir esta expresión debemos recordar que un radián es el ángulo central que intercepta sobre la circunferencia un arco de longitud igual al radio. Por tanto, si un ángulo central φ se mide en radianes, debe cumplirse que
φ =
arco / radio
=
s / r
de donde
s = φ · r

Sabemos, por otra parte, que la velocidad lineal vale, por definición:
v =
lim Δ t→0
Δr→ / Δt


relación velocidad lineal y angular

En el límite, cuando Δt tiende a cero, el vector desplazamiento Δr→ tiende a convertirse en el arco Δs, de donde resulta finalmente la relación entre las dos velocidades:

v =
lim Δ t→0
Δr→ / Δt
=
Δs / Δt
=
Δφ · r / Δt
=
Δφ / Δt
· r = ω · r


Unidades de la velocidad angular
Teniendo en cuenta que φ = s/r determinamos la ecuación de dimensiones de la velocidad angular:

[ω] =
[φ] / [t]
=
[s] / [r] / [t]
=
L / L / T
=
1 / T
= T-1

De donde se deduce que la unidad es el radián/segundo (rad/s) o simplemente el s-1. Aunque también se suele medir en revoluciones por minuto (rev/min o rpm).


Periodo y frecuencia
El MCU es un movimiento periódico porque cada cierto intervalo de tiempo constante, al que llamamos periodo, una partícula dada vuelve a su posición anterior. El periodo T es el tiempo necesario para que una partícula gire una circunferencia completa.
Su valor se deduce fácilmente si recordamos que un giro completo equivale a 2 π radianes, de modo que en la expresión
ω =
φ / t

si φ = 2 π, el tiempo es, por definición, el periodo T y resulta que
ω =
2 π / T
de donde
  • T =
    2 π / ω
cuya unidad es el s/rev.

La frecuencia N es el número de revoluciones dadas en la unidad de tiempo. Su valor es el recíproco o inverso del periodo:
  • N =
    1 / T
    =
    ω / 2 π

Se mide en rev/s, o ciclos/s, unidad a la que damos el nombre de hertz (Hz).


Movimiento Vertical Movimiento Circular Uniformemente Acelerado (MCUA)