Matemáticas ⇒ Matrices ⇒ Cálculo del Rango de una Matriz
El método de Gauss consiste en transformar la matriz, mediante operaciones elementales con las filas, en otra matriz que sea escalonada.| 1 | 9 | 2 | 6 | 7 | 4 | 0 | 3 |
| 0 | 8 | 1 | 5 | 2 | 0 | 2 | 7 |
| 0 | 0 | 0 | 1 | 0 | 5 | 1 | 4 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 2 |
- Una matriz escalonada es aquella en la que el número de ceros que precede al primer elemento distinto de cero de cada fila es mayor que en la fila anterior.
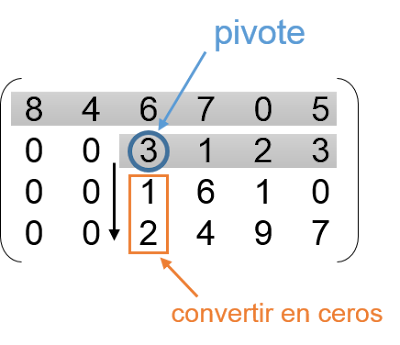
Para escalonar la matriz, se van haciendo ceros por debajo del elemento no nulo más a la izquierda que se pueda encontrar en cada fila, apoyándose en este (pivote), de izquierda a derecha y de arriba abajo.
Una vez obtenida la matriz escalonada, el rango de la matriz equivale al número de filas no nulas de ésta. Se sabe que las filas nulas son linealmente dependientes de las demás.
Ejemplo
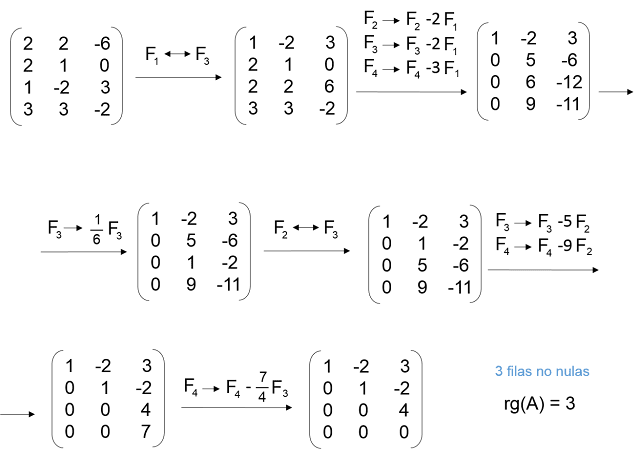
Hallemos el rango de la matriz:
| 2 | 2 | - 6 |
| 2 | 1 | 0 |
| 1 | - 2 | 3 |
| 3 | 3 | - 2 |
siendo conveniente apuntar las operaciones elementales realizadas en cada paso para mantener el rigor.
| Operaciones elementales | Matriz Inversa - Método de Gauss-Jordan |