Regla de L'Hôpital - Ejercicios

Matemáticas ⇒ Derivación ⇒ Regla de L'Hôpital

Sean f y g dos funciones que cumplan una de las siguientes condiciones:

• lim f (x) = lim g (x) = 0
• lim f (x) = ± lim g (x) = ± ∞

Si existe lim

f ' (x) / g ' (x)

, sea finito o infinito, entonces:

lim f (x) / g (x) = lim f ' (x) / g ' (x)

Esta regla sirve para resolver directamente indeterminaciones del tipo

0 / 0

o

±∞ / ±∞

, veamos las posibilidades en los siguientes ejercicios resueltos:


Indeterminaciones del tipo

0 / 0

o

±∞ / ±∞

lim x→2 (x – 2) 3 / sen (x – 2) = lim x→2 3 · (x – 2) 2 / cos (x – 2) = 0 / 1 = 0 lim x→∞ 3x 2 – 5 / ln x = lim x→∞ 6 · x / 1 / x = lim x→∞ 6 · x 2 = ∞

Indeterminaciones del tipo ∞ – ∞
Hay que realizar la resta para que la indeterminación se convierta en una de las anteriores.

lim x→0+ 1 / sen x – 1 / x = lim x→0+ x – sen x / x sen x = lim x→0+ 1 – cos x / sen x + x cos x = lim x→0+ sen x / cos x + cos x – x sen x = 0 / 2 = 0

Indeterminaciones del tipo 0 · (±∞)
Podemos transformar el límite en dos maneras distintas:

lim x→∞ x · sen 3 / x = lim x→∞ sen 3 / x / 1 / x = = lim x→∞ cos 3 / x · – 3 / x2 / – 1 / x2 = lim x→∞ 3 cos 3 / x = 3

Indeterminaciones del tipo 1^±∞, 0⁰ y ∞⁰
Se llamaría L al límite pedido y luego se toman logaritmos:

lim x→0 (x + 1)1/2x L = lim x→0 (x + 1)1/2x ln L = ln lim x→0 (x + 1)1/2x ln L = lim x→0 ln (x + 1)1/2x ln L = lim x→0 1 / 2x ln (x + 1) = lim x→0 ln (x + 1) / 2x = = lim x→0 1 / (x + 1) / 2 = lim x→0 1 / 2x + 2 = 1 / 2 ln L = 1 / 2   ⇒   L = e1/2 = √e

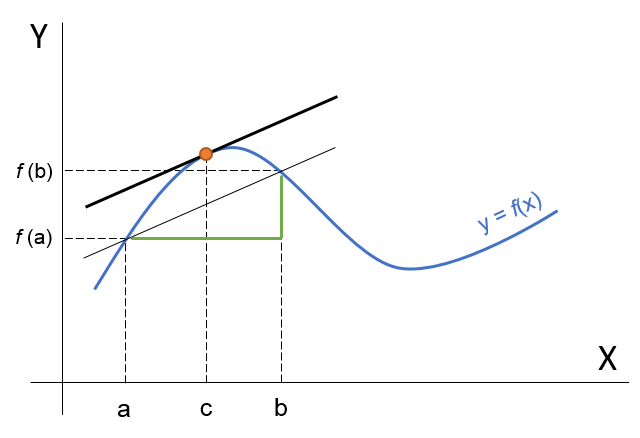
Teorema del valor medio del cálculo diferencial

Problemas de Optimización

Teorema del valor medio del cálculo diferencial

Matemáticas ⇒ Derivación ⇒ Teorema del valor medio

Si una función f es continua en el intervalo cerrado [a, b] y derivable en el correspondiente intervalo abierto (a, b), entonces existe al menos un punto c ∈ (a, b) tal que: f ' (c) = f (b) – f (a) / b – a

Interpretación geométrica
Cumplidas las hipótesis, el teorema afirma la existencia de al menos un punto en el intervalo (a, b) en el que la tangente es paralela a la recta que une los puntos en la gráfica de a y b.

Teorema de Rolle

Regla de L'Hôpital

Teorema de Rolle

Matemáticas ⇒ Derivación ⇒ Teorema de Rolle

Si una función f es continua en el intervalo cerrado [a, b] y derivable en el correspondiente intervalo (a,b) y además f (a) = f (b), entonces existe al menos un punto c ∈ (a, b) tal que f ' (c) = 0.

Interpretación geométrica
El teorema concluye que si dicha función cumple las hipótesis, ha de existir algún punto en el intervalo (a, b) en el que la tangente sea horizontal. Simplemente garantiza su existencia.

Método general para calcular extremos y puntos de inflexión

Teorema del valor medio del cálculo diferencial

Método general para calcular extremos y puntos de inflexión

Matemáticas ⇒ Derivación ⇒ Cálculo de extremos y puntos de inflexión

Si para una función f se verifica:

f ' (x₀)  ;  f '' (x₀)  ;  f ''' (x₀) = 0  ; ··· ;  f ^{(n – 1)} (x₀) = 0  ; 
pero f ⁿ (x₀) ≠ 0, entonces:

• Si n es par; f tiene un extremo relativo en x₀, que es máximo relativo si f ⁿ (x₀) < 0 o mínimo si f ⁿ (x₀) > 0.
• Si n es impar; f tiene un punto de inflexión en x₀.

Ejercicio resuelto
Hallar extremos y/o puntos de inflexión de la función: f (x) = x⁵ – 8

f ' (x) = 5·x4   ;   x = 0   ⇒   f ' (0) = 0 Tenemos un punto crítico en x = 0, profundicemos para saber si es extremo relativo o punto de inflexión: f '' (x) = 20·x3   ⇒   f '' (0) = 0 f ''' (x) = 60·x2   ⇒   f ''' (0) = 0 f 4 (x) = 120·x   ⇒   f 4 (0) = 0 f 5 (x) = 120   ⇒   f 5 (0) = 120 ≠ 0 Concluimos que la función f tiene un punto de inflexión en x = 0.

Puntos de inflexión

Teorema de Rolle

Puntos de inflexión - Ejemplo

Matemáticas ⇒ Derivación ⇒ Puntos de inflexión

Dada una función f:

• Si para f ''(x₀) = 0 y f ''' (x₀) ≠ 0; se dice que f tiene un punto de inflexión en x₀. La función cambia su concavidad en ese punto.

Ejercicio resuelto
Hallar los puntos de inflexión de la función: f (x) = sen x

f ' (x) = cos x   ⇒   f '' (x) = –sen x   ⇒   f ''' (x) = –cos x Calculamos posibles puntos de inflexión: f '' (x) = 0   ⇒   –sen x = 0 x1 = 0 + 2·π·k  ;  x2 = π + 2·π·k Verificamos que la derivada tercera en estos puntos es distinta de cero: f ''' (x1) = –cos ( 0 + 2·π·k ) = –1 ≠ 0 f ''' (x2) = –cos ( π + 2·π·k ) = 1 ≠ 0 Concluimos que la función f (x) = sen x tiene puntos de inflexión en 0, π y múltiplos de 2π de éstos.

Concavidad de una función

Método general para calcular extremos y puntos de inflexión

Concavidad de una función

Matemáticas ⇒ Derivación ⇒ Concavidad

Si una función f tiene derivada en un punto x₀, entonces se dice que:

• Si f '' (x₀) > 0; f es convexa (o cóncava positiva) en x₀.
• Si f '' (x₀) < 0; f es cóncava (o cóncava negativa) en x₀.

Siguiendo un razonamiento similar con los extremos, se comprueba:

• f '' (x₀) > 0   ⇒   f ' crece en x₀   ⇒   la pendiente de las tangentes aumenta según se incrementa x, así decimos que es convexa en x₀.
• f '' (x₀) < 0   ⇒   f ' decrece en x₀   ⇒   la pendiente de las tangentes disminuye según se incrementa x, así decimos que es cóncava en x₀.

Extremos relativos

Puntos de inflexión

Extremos relativos - Derivada

Matemáticas ⇒ Derivación ⇒ Extremos Relativos

Si existe derivada de la función f en un punto x₀ se dice que:

• Si f ' (x₀) = 0 y f '' (x₀) < 0; f tiene un máximo relativo en x₀.
• Si f ' (x₀) = 0 y f '' (x₀) > 0; f tiene un mínimo relativo en x₀.

Anteriormente, estudiando la monotonía, veíamos que cuando el valor de la derivada era positivo la función era estrictamente creciente y viceversa... Ahora, cuando advertimos que la derivada en un punto es igual a cero, concluimos que la recta tangente a f en ese punto es horizontal.
Aparte, para distinguir entre si es un extremo máximo o mínimo:

• f '' (x₀) < 0   ⇒   f ' es decreciente en x₀   ⇒   las rectas tangentes disminuyen su inclinación a medida que aumenta x, lo que implica un máximo relativo en x₀
• f '' (x₀) > 0   ⇒   f ' es creciente en x₀   ⇒   las rectas tangentes aumentan su inclinación a medida que aumenta x, lo que implica un mínimo relativo en x₀

Nota: una función no tiene por qué tener un extremo en un punto si su derivada en ese punto es cero y su segunda derivada también. Para más información, estudia el método general para calcular extremos y puntos de inflexión.

Monotonía

Concavidad de una función

Monotonía - Derivación

Matemáticas ⇒ Derivación ⇒ Monotonía

Si una función f tiene derivada en un punto x₀, se dice que:

• si f ' (x₀) > 0; f es estrictamente creciente en x₀
• si f ' (x₀) < 0; f es estrictamente decreciente en x₀

La demostración geométrica es trivial

Derivación logarítmica

Extremos relativos

Derivación logarítmica

Matemáticas ⇒ Derivación ⇒ Derivación logarítmica

A la hora de derivar funciones del estilo f = g ^h (h también es una función, no una constante), usamos la derivación logarítmica. Esta técnica consiste en:

• Aplicar logaritmos neperianos:

ln f = ln g ^h   ⇒   ln f = h · ln g

• Tratar cada miembro de la ecuación como una función y derivar:


f ' / f
= h ' · ln g + h ·
g ' / g


• Finalmente, se despeja f ':
  f ' = f · ( h ' · ln g + h ·
  g ' / g
  )

No es necesario memorizar y mecanizar todo el proceso, basta con saber que hay que aplicar logaritmos cuando la base y el exponente dependan de x. El resto de cálculos saldrán como por arte de magia.


Ejercicio resuelto
Sea f (x) = x ^{cos x}, hallar f ' (x).

ln f (x) = ln x cos x   ⇒   ln f (x) = cos x · ln x   ⇒   f ' (x) / f (x) = – sen x · ln x + cos x · 1 / x   ⇒   f ' (x) = f (x) · ( – sen x · ln x + cos x · 1 / x ) = x cos x · ( – sen x · ln x + cos x · 1 / x )

Regla de la cadena

Monotonía

Regla de la cadena - Derivación

Matemáticas ⇒ Derivación ⇒ Regla de la cadena

La composición de dos funciones f y g se deriva siguiendo la fórmula:

(g o f ) ' (x) = g ' (f (x)) · f ' (x)

Ejercicio resuelto
Obtener la función derivada de h(x) = cos (sen x)

• g (x) = cos x
• f (x) = sen x
• h (x) = (g o f) (x) = cos (sen x)

h ' (x) = (g o f ) ' (x) = g ' (f (x)) · f ' (x) = – sen (sen x) · cos x

Reglas de derivación

Derivación logarítmica

Reglas de derivación

Matemáticas ⇒ Derivación ⇒ Reglas de derivación

Derivada de una función por un escalar

(kf) ' (x) = kf ' (x)

Derivada de una suma

(f + g) ' (x) = f ' (x) + g ' (x)

Derivada de un producto

(f · g) ' (x) = f ' (x) · g (x) + f (x) · g ' (x)

Derivada de un cociente

( f / g ) ' (x) = f ' (x) · g (x) – f (x) · g ' (x) / [g (x)] 2

Tabla de Derivadas

Regla de la cadena

Tabla de Derivadas

Matemáticas ⇒ Derivación ⇒ Tabla de derivadas

FUNCIÓN	DERIVADA
f (x) = k	f ' (x) = 0
f (x) = x n	f ' (x) = n x n – 1
f (x) = n√x	f ' (x) = 1 / n n√x n – 1
f (x) = sen x	f ' (x) = cos x
f (x) = cos x	f ' (x) = – sen x
f (x) = tg x	f ' (x) = 1 / cos2 x
f (x) = e x	f ' (x) = e x
f (x) = a x	f ' (x) = a x ln a
f (x) = ln x	f ' (x) = 1 / x
f (x) = log a x	f ' (x) = 1 / x ln a
f (x) = arcsen x	f ' (x) = 1 / √1 – x2
f (x) = arccos x	f ' (x) = –1 / √1 – x2
f (x) = arctg x	f ' (x) = 1 / 1 + x2

Tabla de integrales inmediatas

Definición de derivada

Reglas de derivación

Definición de derivada

Matemáticas ⇒ Derivación ⇒ Definición de derivada

La derivada de una función f en un punto x₀ es el valor del límite, si existe y es finito:

f ' (x0) = lim h→0 f (x0 + h) – f (x0) / h

Interpretación geométrica
El cociente  

f (x₀ + h) – f (x₀) / h

 equivale a la pendiente de la recta en la gráfica de f que pasa por los puntos x₀ y (x₀ + h). Si disminuimos el tamaño de h, la recta se aproxima a una recta tangente a la gráfica en el punto x₀.

La derivada de la función f en el punto x₀ es la pendiente de la recta tangente a f en el punto x₀.




Definición alternativa

f '(x0) = lim x → x0 f(x) – f(x0) / x – x0

Tabla de Derivadas

Derivación

Matemáticas ⇒ Derivación

Cálculo de derivadas

• Definición de derivada
• Tabla de derivadas
• Reglas de derivación
• Regla de la cadena
• Derivación logarítmica

Estudio de una función mediante derivadas

• Monotonía
• Extremos relativos
• Concavidad
• Puntos de inflexión
• Método general para calcular extremos y puntos de inflexión

Propiedades de las funciones derivables

• Teorema de Rolle
• Teorema del valor medio del cálculo diferencial

Aplicaciones de las derivadas

• Regla de L'Hôpital
• Optimización

Arcotangente

Matemáticas ⇒ Trigonometría ⇒ Arcotangente

Por definición, el arcotangente es la función recíproca de tangente. No confundir con la razón cotangente, que es la inversa. En un triángulo rectángulo equivale al ángulo que corresponde al cociente del cateto opuesto entre el cateto contiguo.

arctg cateto opuesto / cateto contiguo = α

• arctg (tg α) = α

Dominio
Si se tienen en cuenta los inputs y outputs de la función, se concluye que el arcotangente admite cualquier valor devuelve ángulos entre –90º y 90º.

• Apunte: en calculadoras o programas informáticos es posible encontrarse con tan^–1, que hace referencia al arcotangente. Los informáticos no aparentan tener sabiduría trigonométrica, ya que tg^–1 α =
  1 / tg α
  = cotg α . Ante la duda, conviene comprobar: si tan^–1 (1) = 45º, entonces se puede calcular el arcotangente con esa función. Cuidado con la diferencia de conceptos, el matiz es muy importante.

Arcocoseno

Teorema de los senos

Arcocoseno

Matemáticas ⇒ Trigonometría ⇒ Arcocoseno

Por definición, el arcocoseno es la función recíproca del coseno. No confundir con la razón secante, que es la inversa. En un triángulo rectángulo equivale al ángulo que corresponde al cociente del cateto contiguo entre la hipotenusa.

arccos cateto contiguo / hipotenusa = α

• arccos (cos α) = α

Dominio
Si se tienen en cuenta los inputs y outputs de la función, se concluye que el arcocoseno admite valores comprendidos entre –1 y 1 y devuelve ángulos entre 0º y 180º.

• Apunte: en calculadoras o programas informáticos es posible encontrarse con cos^–1, que hace referencia al arcocoseno. Los informáticos no aparentan tener sabiduría trigonométrica, ya que cos^–1 α =
  1 / cos α
  = sec α . Ante la duda, conviene comprobar: si cos^–1 (0) = 90º, entonces se puede calcular el arcocoseno con esa función. Cuidado con la diferencia de conceptos, el matiz es muy importante.

Arcoseno

Arcotangente

Arcoseno

Matemáticas ⇒ Trigonometría ⇒ Arcoseno

Por definición, el arcoseno es la función recíproca del seno. No confundir con la razón cosecante, que es la inversa. En un triángulo rectángulo equivale al ángulo que corresponde al cociente del cateto opuesto entre la hipotenusa.

arcsen cateto opuesto / hipotenusa = α

• arcsen (sen α) = α

Dominio
Si se tienen en cuenta los inputs y outputs de la función, se concluye que el arcoseno admite valores comprendidos entre –1 y 1 y devuelve ángulos entre –90º y 90º.

• Apunte: en calculadoras o programas informáticos es posible encontrarse con sin^–1, que hace referencia al arcoseno. Los informáticos no aparentan tener sabiduría trigonométrica, ya que sen^–1 α =
  1 / sen α
  = cosec α . Ante la duda, conviene comprobar: si sin^–1 (1) = 90º, entonces se puede calcular el arcoseno con esa función. Cuidado con la diferencia de conceptos, el matiz es muy importante.

Ángulo Doble y Mitad

Arcoseno

Identidades Trigonométricas Fundamentales

Matemáticas ⇒ Trigonometría ⇒ Identidades Trigonométricas Fundamentales

cos² α + sen² α = 1


sec² α = 1 + tg² α


cosec² α = 1 + cotg² α

Fórmula Fundamental de la Trigonometría

Suma y diferencia de ángulos

Convenio de ángulos - Trigonometría

Matemáticas ⇒ Trigonometría ⇒ Convenio de ángulos

Un ángulo es básicamente el lugar geométrico del plano que abarcan dos rectas, se suele denotar con una letra griega:

Medición de ángulos
Consideramos el ángulo positivo si lo medimos en sentido antihorario, y negativo en sentido horario. Para asignar un valor numérico, es común usar el sistema sexagesimal en el que una "vuelta completa" está dividida en 360 partes. Cada parte es un grado (º), así, dos rectas perpendiculares formarían un ángulo de 90º. Un grado está dividido en 60 minutos ('), y cada minuto está formado a su vez por 60 segundos (''). Si, por ejemplo, medimos un ángulo con el sistema sexagesimal y somos precisos obtendríamos:

12º 34' 56,789''    podemos meter todos los decimales que queramos en los segundos...


Radianes
En matemáticas a veces es más cómodo medir la amplitud de un ángulo con radianes. Por definición, un radián es la región del plano que abarca un arco de circunferencia cuya longitud es la misma que el radio de tal circunferencia.

En consecuencia, una "vuelta completa" tiene un ángulo de 2π radianes (ya que la longitud total de una circunferencia es 2π·radio). Si asumimos la equivalencia 2π rad = 360º, podemos aplicar la conversión de unidades y obtener el valor de un radián en grados:

1 rad = 53º 17' 44,81''

• Dato interesante: la trigonometría sería más digestible si se considerase el ángulo de una "vuelta completa" como τ (tau) radianes, siendo τ = 2 π ≈ 6,28. Esto simplificaría muchísimo la localización en la circunferencia goniométrica, por ejemplo: un cuarto de vuelta implica un ángulo de τ/4, mucho más asimilable que decir π/2. Y no solo en trigonometría, el número 2π aparece en una gran variedad de fórmulas matemáticas que quedarían más elegantes si se les colocara el equivalente τ. Por desgracia, para estar acorde con el "mundo real" de la academia, aprenderemos trigonometría con el obsoleto número π... Y si no te gusta, no te preocupes en cambiar: ni el profesor ni el sistema educativo lo harán.

Circunferencia Goniométrica

Circunferencia Goniométrica - Trigonometría

Matemáticas ⇒ Trigonometría ⇒ Circunferencia Goniométrica

La circunferencia goniométrica es simplemente una circunferencia de radio 1.

Se suele usar para estudiar las razones trigonométricas proyectando triángulos rectángulos en ella. Por ejemplo, para el coseno tenemos:

Para comprender los cambios de signo de una función trigonométrica dividimos la circunferencia en cuatro cuadrantes, y los nombramos en sentido antihorario, el mismo utilizado en el convenio de ángulos.

Por ejemplo, el signo del seno en cada cuadrante es:

La circunferencia goniométrica también se conoce con el nombre de circunferencia trigonométrica, unitaria o "círculo unidad".

Convenio de ángulos

Seno

Trigonometría - Cotangente

Matemáticas ⇒ Trigonometría ⇒ Cotangente

Nota: no confundir con el arcotangente.

Por definición, la cotangente de un ángulo es el inverso de la tangente de dicho ángulo:

cotg α = 1 / tg α = cos α / sen α

La cotangente en la circunferencia goniométrica

Signo de la cotangente

Cotangente de ángulo suplementario

• cotg (180º – α) = cotg (π – α) = – cotg α

Cotangente de ángulo complementario

• cotg (90º – α) = cotg (π/2 – α) = tg α

Cotangente de ángulo opuesto (negativo)

• cotg (– α) = – cotg α

Cotangente de ángulos que se diferencian en 180º

• cotg (180º + α) = cotg (π + α) = cotg α

Cotangente de ángulos que se diferencian en 90º

• cotg (90º + α) = cotg (π/2 + α) = – tg α

Secante

Razones Trigonométricas de algunos ángulos

Trigonometría - Secante

Matemáticas ⇒ Trigonometría ⇒ Secante

Nota: no confundir con la cosecante ni con el arcocoseno.

Por definición, la secante de un ángulo es el inverso del coseno de dicho ángulo:

sec α = 1 / cos α

La secante en la circunferencia goniométrica

Signo de la secante

Secante de ángulo suplementario

• sec (180º – α) = sec (π – α) = – sec α

Secante de ángulo complementario

• sec (90º – α) = sec (π/2 – α) = cosec α

Secante de ángulo opuesto (negativo)

• sec (– α) = sec α

Secante de ángulos que se diferencian en 180º

• sec (180º + α) = sec (π + α) = – sec α

Secante de ángulos que se diferencian en 90º

• sec (90º + α) = sec (π/2 + α) = – cosec α

Cosecante

Cotangente

Trigonometría - Cosecante

Matemáticas ⇒ Trigonometría ⇒ Cosecante

Nota: no confundir con la secante ni con el arcoseno.

Por definición, la cosecante de un ángulo es el inverso del seno de dicho ángulo:

cosec α = 1 / sen α

La cosecante en la circunferencia goniométrica

Signo de la cosecante

Cosecante de ángulo suplementario

• cosec (180º – α) = cosec (π – α) = cosec α

Cosecante de ángulo complementario

• cosec (90º – α) = cosec (π/2 – α) = sec α

Cosecante de ángulo opuesto (negativo)

• cosec (– α) = – cosec α

Cosecante de ángulos que se diferencian en 180º

• cosec (180º + α) = cosec (π + α) = – cosec α

Cosecante de ángulos que se diferencian en 90º

• cosec (90º + α) = cosec (π/2 + α) = sec α

Tangente

Secante

Trigonometría - Tangente

Matemáticas ⇒ Trigonometría ⇒ Tangente

Por definición, la tangente de un ángulo es el cociente del cateto opuesto entre el cateto contiguo de un triángulo rectángulo:

tg α = cateto opuesto / cateto contiguo

En consecuencia:

tg α = cateto opuesto / cateto contiguo = cateto opuesto / hipotenusa / cateto contiguo / hipotenusa = sen α / cos α

La tangente en la circunferencia goniométrica

Signo de la tangente

Tangente de ángulo suplementario

• tg (180º – α) = tg (π – α) = – tg α

Tangente de ángulo complementario

• tg (90º – α) = tg (π/2 – α) = cotg α

Tangente de ángulo opuesto (negativo)

• tg (– α) = – tg α

Tangente de ángulos que se diferencian en 180º

• tg (180º + α) = tg (π + α) = tg α

Tangente de ángulos que se diferencian en 90º

• tg (90º + α) = tg (π/2 + α) = – cotg α

Coseno

Cosecante

Trigonometría - Coseno

Matemáticas ⇒ Trigonometría ⇒ Coseno

Por definición, el coseno de un ángulo es el cociente del cateto contiguo entre la hipotenusa de un triángulo rectángulo:

cos α = cateto contiguo / hipotenusa

El coseno en la circunferencia goniométrica

Signo del coseno

Coseno de ángulo suplementario

• cos (180º – α) = cos (π – α) = – cos α

Coseno de ángulo complementario

• cos (90º – α) = cos (π/2 – α) = sen α

Coseno de ángulo opuesto (negativo)

• cos (– α) = cos α

Coseno de ángulos que se diferencian en 180º

• cos (180º + α) = cos (π + α) = – cos α

Coseno de ángulos que se diferencian en 90º

• cos (90º + α) = cos (π/2 + α) = – sen α

Seno

Tangente

Trigonometría - Seno

Matemáticas ⇒ Trigonometría ⇒ Seno

Por definición, el seno de un ángulo es el cociente del cateto opuesto entre la hipotenusa de un triángulo rectángulo:

sen α = cateto opuesto / hipotenusa

El seno en la circunferencia goniométrica

Signo del seno

Seno de ángulo suplementario

• sen (180º – α) = sen (π – α) = sen α

Seno de ángulo complementario

• sen (90º – α) = sen (π/2 – α) = cos α

Seno de ángulo opuesto (negativo)

• sen (– α) = – sen α

Seno de ángulos que se diferencian en 180º

• sen (180º + α) = sen (π + α) = – sen α

Seno de ángulos que se diferencian en 90º

• sen (90º + α) = sen (π/2 + α) = cos α

La Circunferencia Goniométrica

Coseno

Trigonometría - Teorema del coseno

Matemáticas ⇒ Trigonometría ⇒ Teorema del coseno

Para cualquier triángulo se cumple lo siguiente (basta recordar solo una ecuación ya que las otras dos son análogas):

a2 = b2 + c2 – 2 b c cos A
b2 = c2 + a2 – 2 c a cos B
c2 = a2 + b2 – 2 a b cos C

Demostración

• cos C =
  x / b
    ⇒   x = b cos C
• b² = h² + x²   ⇒   x² = b² – h²


• (a – x)² + h² = c²   ⇒

⇒   a² – 2·a·x + x² + h² = c²   ⇒

⇒   a² – 2·a·b·cos C + b² – h² + h² = c²   ⇒



c2 = a2 + b2 – 2 a b cos C

Teorema de los senos

Trigonometría - Teorema de los senos

Matemáticas ⇒ Trigonometría ⇒ Teorema de los senos

Para cualquier triángulo se cumple:

a / sen A = b / sen B = c / sen C

Demostración: puro fácil

sen B =

h / c

     sen C =

h / b

⇒   h = c sen B = b sen C   ⇒  

b / sen B

=

c / sen C

Por analogía:

a / sen A = b / sen B = c / sen C

Arcotangente

Teorema del coseno

Trigonometría - Ángulo Doble y Mitad

Matemáticas ⇒ Trigonometría ⇒ Ángulo Doble y Mitad

Ángulo Doble

• sen 2α = 2 sen α cos α


• cos 2α = cos² α – sen² α


• tg 2α =
  2 tg α / 1 – tg² α

Ángulo Mitad

• sen
  α / 2
  = √
  1 – cos α / 2


• cos
  α / 2
  = √
  1 + cos α / 2


• tg
  α / 2
  = √
  1 – cos α / 1 + cos α

Suma y diferencia de ángulos

Arcoseno

Trigonometría - Suma y diferencia de ángulos

Matemáticas ⇒ Trigonometría ⇒ Suma y diferencia de ángulos

Seno de una suma

• sen(α + β) = sen α cos β + sen β cos α

Coseno de una suma

• cos(α + β) = cos α cos β – sen α sen β

Tangente de una suma

• tg(α + β) =
  tg α + tg β / 1 – tg α tg β

Seno de una resta

• sen(α – β) = sen α cos β – cos α sen β

Coseno de una resta

• cos(α – β) = cos α cos β + sen α sen β

Tangente de una resta

• tg(α – β) =
  tg α – tg β / 1 + tg α tg β

Identidades Trigonométricas Fundamentales

Ángulo Doble y Mitad

Razones Trigonométricas de los ángulos de 30º, 45º y 60º

Matemáticas ⇒ Trigonometría ⇒ Relaciones de algunos ángulos

α	0º	30º	45º	60º	90º
	0	π / 6	π / 4	π / 3	π / 2
sen α	0	1 / 2	√2 / 2	√3 / 2	1
cos α	1	√3 / 2	√2 / 2	1 / 2	0
tg α	0	√3 / 3	1	√3	–

Los valores de la tabla se pueden probar si se tienen en cuenta los siguientes triángulos sacados de un cuadrado y un triángulo equilátero:

Cotangente

Fórmula Fundamental de la Trigonometría

Fórmula Fundamental de la Trigonometría

Matemáticas ⇒ Trigonometría ⇒ Fórmula Fundamental

sen2 α + cos2 α = 1

Demostración

Para este triángulo rectángulo, aplicamos el Teorema de Pitágoras:

• hipotenusa² = (cateto opuesto)² + (cateto contiguo)²

Y simplemente, teniendo en mente las definiciones de seno y coseno, dividimos ambos miembros por hipotenusa²:

• hipotenusa² / hipotenusa²
  =
  (cateto opuesto)² / hipotenusa²
  +
  (cateto contiguo)² / hipotenusa²
• 1 = sen² α + cos² α

Nota: sen² α = (sen α)²

Razones trigonométricas de algunos ángulos

Identidades Trigonométricas Fundamentales