Física ⇒ Rotación del Sólido Rígido ⇒ Trabajo de Rotación
El trabajo en la rotación es igual al producto del momento de la fuerza exterior aplicada por el ángulo girado, en radianes.| W1 - 2 = θ2 ∫ θ1 Mo dθ = Mo (θ2 – θ1) |
|---|
El trabajo realizado por un momento exterior aplicado en un sólido rígido es igual a la variación de su energía cinética de rotación.
|
Mo (θ2 – θ1) =
1
2
I ω22 –
1
2
I ω12
|
|---|
La potencia en la rotación se define: P =
dW
dt
= Mo ·
dθ
dt
= Mo · ωDemostración
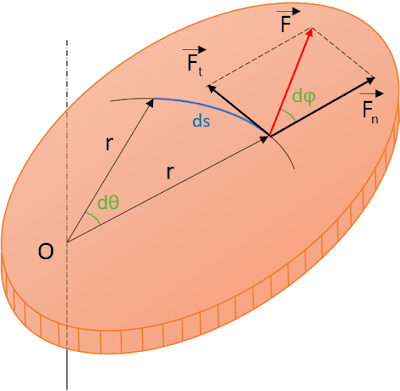
Cuando un cuerpo adquiere una energía cinética, dicha energía debe proceder bien de otra energía o bien de un trabajo aplicado al cuerpo. La componente tangencial Ft es la componente de F que solo realiza trabajo, ya que Fn es perpendicular a la trayectoria. En un desplazamiento ds, el trabajo realizado por la fuerza F es:
ds = r dθ ⇒ dW = F sen φ · r · dθ
Como F · r · sen φ es el momento de la fuerza F respecto del punto O, se obtiene para el trabajo elemental: dW = Mo dθ
| Energía Cinética de Rotación | Momento Angular del Sólido Rígido |