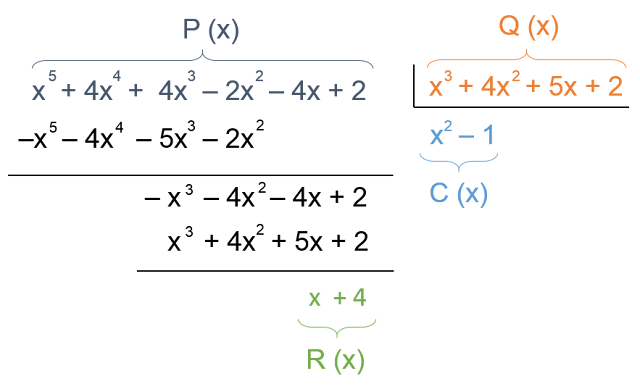Matemáticas ⇒ Integrales Indefinidas ⇒ Integración de funciones racionales
Aunque existe un método general para resolver integrales de funciones racionales tipo:
P (x)
Q (x)
dx
Daremos dos casos específicos que serán muy útiles:
P (x)
Q (x)
como suma de fracciones simples, así la integral se reduce a una suma de integrales inmediatas.Ejercicio resuelto Calcular la integral ∫
x + 4
x3 + 4x2 + 5x + 2
dxLa fracción que queremos integrar ya está descompuesta como suma de fracciones simples en este apartado.
x + 4
x3 + 4x2 + 5x + 2
=
x + 4
(x + 2) · (x + 1)2
=
2
x + 2
+
–2
x + 1
+
3
(x + 1)2
Luego:
x + 4
x3 + 4x2 + 5x + 2
dx =
∫
2
x + 2
dx +
∫
–2
x + 1
dx +
∫
3
(x + 1)2
dx = = 2 ln |x + 2| – 2 ln |x + 1| + 3
(x + 1)–1
–1
+ C = 2 ln |x + 2| – 2 ln |x + 1| –
3
x + 1
+ C
|
la integral ∫
R (x)
Q (x)
dx tiene el numerador con menor grado que el del denominador, así que resuelve siguiendo el último apartado.
Ejercicio resuelto Calcular la integral ∫
x5 + 4x4 + 4x3 – 2x2 – 4x + 2
x3 + 4x2 + 5x + 2
dx
x5 + 4x4 + 4x3 – 2x2 – 4x + 2
x3 + 4x2 + 5x + 2
dx =
∫
(x2 – 1) dx +
∫
x + 4
x3 + 4x2 + 5x + 2
dx
La primera integral es un polinomio y la segunda es la misma que se resolvió en el ejercicio anterior. Entonces:
x5 + 4x4 + 4x3 – 2x2 – 4x + 2
x3 + 4x2 + 5x + 2
dx =
x3
3
– x + 2 ln |x + 2| – 2 ln |x + 1| –
3
x + 1
+ C
|
| Descomposición de una fracción | Integración por cambio de variable |