Física ⇒ Dinámica de los sistemas de partículas ⇒ Teorema de las Áreas
| En el movimiento de un cuerpo bajo la acción de una fuerza central su momento angular es constante y, además, el vector de posición respecto del centro de la fuerza barre áreas iguales en tiempos iguales. |
|---|
Segunda ley de Kepler
El señor Kepler observó el sistema solar y de sus resultados experimentales se convenció: el radio vector que une el Sol con un planeta barre áreas iguales en tiempos iguales.
Demostración
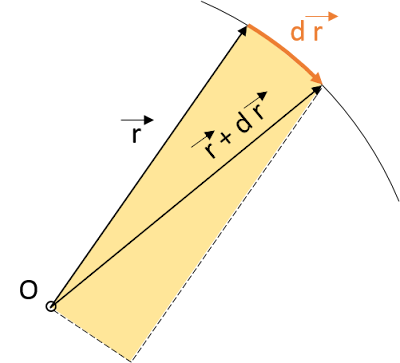
Teniendo en cuenta la relación entre el área y el producto vectorial, calculemos el área dA barrida por el vector de posición r→ en un intervalo de tiempo dt:
Área barrida por r→ = dA =
1
2
|r→ × dr→|Por la definición de velocidad, dr→ = v→ · dt:
dA =
1
2
|r→ × v→ · dt|
dA
dt
=
1
2
|r→ × v→|
Como L = |r→ × v→|, la velocidad areolar expresada en función del momento angular es:
|
dA
dt
=
1
2
L
m
|
|---|
Dado que el momento angular es constante así como la masa del objeto que está en órbita, concluímos:
| La velocidad areolar de una partícula que se mueve bajo la acción de una fuerza central es constante. |
|---|
| Conservación del Momento Angular de una Partícula | Momento Angular de un Sistema de Partículas |