Física ⇒ Dinámica del Punto Material ⇒ Teorema de Conservación del Momento Lineal
Sea un cuerpo sobre el que la resultante de las fuerzas exteriores es nula. Luego, el impulso, F · t, es nulo y no varía el momento lineal del cuerpo.F = 0 ⇒ m · v – m · v0 = 0 ⇒
| m · v = m · v0 |
|---|
- m · v0 = momento lineal inicial
- m · v = momento lineal final
| Si la resultante de las fuerzas exteriores que actúan sobre un cuerpo es nula, el momento lineal de éste permanece constante. |
|---|
Este teorema tiene una interesante aplicación en el caso de un sistema formado por dos o más cuerpos.
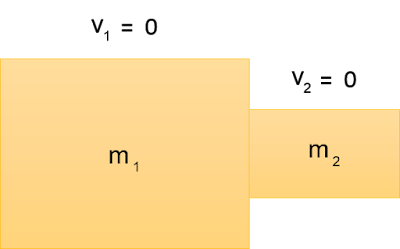
Sea, por ejemplo, un sistema formado por dos cuerpos de masas m1 y m2. Cuando están en reposo, sus velocidades v1 y v2 son nulas y, por ello, su momento lineal total es cero:
Si aplicamos una fuerza interna, como una explosión, las velocidades de los cuerpos v'1 y v'2 ya no son nulas, ni tampoco es nulo el momento lineal de cada cuerpo; pero el teorema de conservación exige que el momento lineal total sea nulo, como lo era al principio:
Lo que significa que los momentos lineales finales de los cuerpos son iguales y de sentido contrario.
| m1 · v'1 = – m2 · v'2 |
|---|
De esta manera, cuando se dispara una escopeta, inicialmente es nulo el momento lineal del sistema arma + proyectil. Al ser disparada, la escopeta retrocede de tal modo que el momento lineal del arma es igual y de sentido contrario al momento lineal del proyectil. Así, el momento lineal del conjunto es nulo como antes de disparar: su valor se ha mantenido constante.
Se puede entender el principio de acción-reacción como un juego de suma cero, en el que se transfiere momento lineal entre cuerpos.
| Teorema del Impulso Lineal | Definición de fuerza de rozamiento |