Física ⇒ Rotación del Sólido Rígido ⇒ Momento de Inercia de una Barra - Cálculo
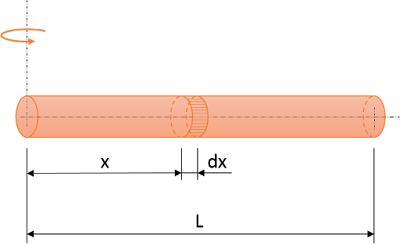
El momento de inercia de una barra homogénea de masa m, longitud L y sección s, respecto de un eje que pasa por el extremo perpendicular a la barra es:|
I =
1
3
· m L2
|
|---|
Cálculo
A una distancia x del eje de giro se toma un elemento diferencial de volumen: dV = s · dx, con masa elemental: dm = ρ · s · dx. Entonces, el momento de inercia que le corresponde a esta masa diferencial es dI = x2 · dm. Así que el momento de inercia total de la barra se obtiene por integración:
|
x3
3
|
1
3
ρ s L3
Y como el volumen de la barra es s · L y la masa, m = ρ · s · L, se obtiene para el momento de inercia de la barra:
1
3
· m L2
Eje que pasa por el centro de masas
El momento de inercia de una barra respecto a un eje que pasa por el centro de masas se puede calcular aplicando el teorema de Steiner en el resultado anterior.
|
I = ICM + m (
L
2
)2
|
|---|
ICM = I – m
L2
4
=
1
3
m L2 –
1
4
m L2|
ICM =
1
12
m L2
|
|---|
| Teorema de Steiner | Momento de Inercia de un Cilindro Macizo |